Lesson 2: Second moment of area
In this lesson, we’ll explore the concept of the Second Moment of Area and understand its significance in mechanical design and engineering.
- What is it Good For?
- The Second Moment of Area serves various purposes in engineering and design:
- Bending resistance of cross sections.
- Selection of the appropriate beam.
- Determining the best installation position.
- Strength analysis.
- It is an indispensable tool in mechanical design.
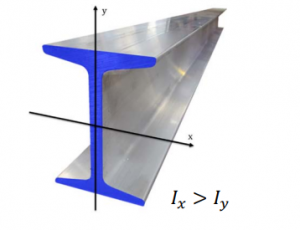
- Definition
- The Second Moment of Area on an axis is a surface integral of a planar object’s area.
- Surface elements are multiplied by the square of their distance from the axis.
- The index ‘I’ specifies the axis to which the Second Moment of Area applies.
- Its value is always positive.
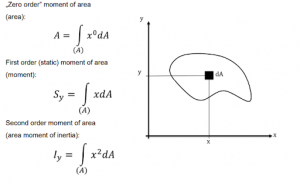
- Second Moment of Area on Two Perpendicular Axes
- The Second Moment of Area on a pair of perpendicular axes is a surface integral of a planar object’s area.
- Surface elements are multiplied by their distances from the axes.
- Two indices of ‘I’ indicate the pair of axes to which it applies.
- Its value can be positive or negative.
- Second Moment of Area Tensor
- The standard units for the Second Moment of Area are m^4, cm^4, mm^4.
- Second Moment of Area on a Point
- The Second Moment of Area on a point is a surface integral of a planar object’s area.
- Surface elements are multiplied by the square of their distance from the point.
- The index ‘I’ specifies the point to which it applies.
- Its value is always positive.
- Parallel Coordinate Transformation
6.1. Steiner’s Theorem for Equatorial Axes
- Steiner’s theorem for equatorial axes allows calculation of the Second Moment of Area on any axis.
- It involves adding the product of the square of the distance between axes and the area of the plane to the Second Moment of Area on a parallel axis passing through the center of gravity.
6.2. Steiner’s Theorem for Perpendicular Axis Pair
- For perpendicular axis pairs, Steiner’s theorem involves adding the product of the object’s area and the distance coordinates of the axes to the centrifugal Second Moment of Area on the centroid.
- Second Moment of Area of a Rectangle
- Learn how to calculate the Second Moment of Area for a rectangular cross-section.
- Second Moment of Area of a Right Triangle
- Discover the process for determining the Second Moment of Area for a right triangle.
- Second Moment of Area of a Sector
- Explore the calculation of the Second Moment of Area for a sector-shaped cross-section.
- Second Moment of Area of a Quarter Circle
- Learn how to calculate the Second Moment of Area for a quarter circle cross-section.
- Second Moment of Area on Rotated Axes
- Understand how to calculate the Second Moment of Area on axes that are not aligned with the object’s natural axes.
Conclusion
- Understand how to calculate the Second Moment of Area on axes that are not aligned with the object’s natural axes.
- Bending resistance: The Second Moment of Area is crucial for analyzing the bending resistance of cross sections, helping ensure the structural integrity of beams and components.
- Design optimization: Engineers can use this concept to select the most suitable beams and installation positions, contributing to efficient and effective mechanical design.
- Strength analysis: It plays a vital role in strength analysis, allowing engineers to assess how materials and components will perform under different loads and stresses.
- Versatility: The Second Moment of Area can be applied to a wide range of geometric shapes and structures, making it a versatile tool in engineering and design.
- Precise calculations: Understanding how to calculate the Second Moment of Area for various shapes and configurations is essential for achieving accurate and reliable results in engineering projects.